Skip to main content

Learning Introductory Physics with Activities

Paul J. Emigh, Rebecka Tumblin, Kathryn Hadley, Danielle Skinner

Section 12.8 Application: The Unicycle

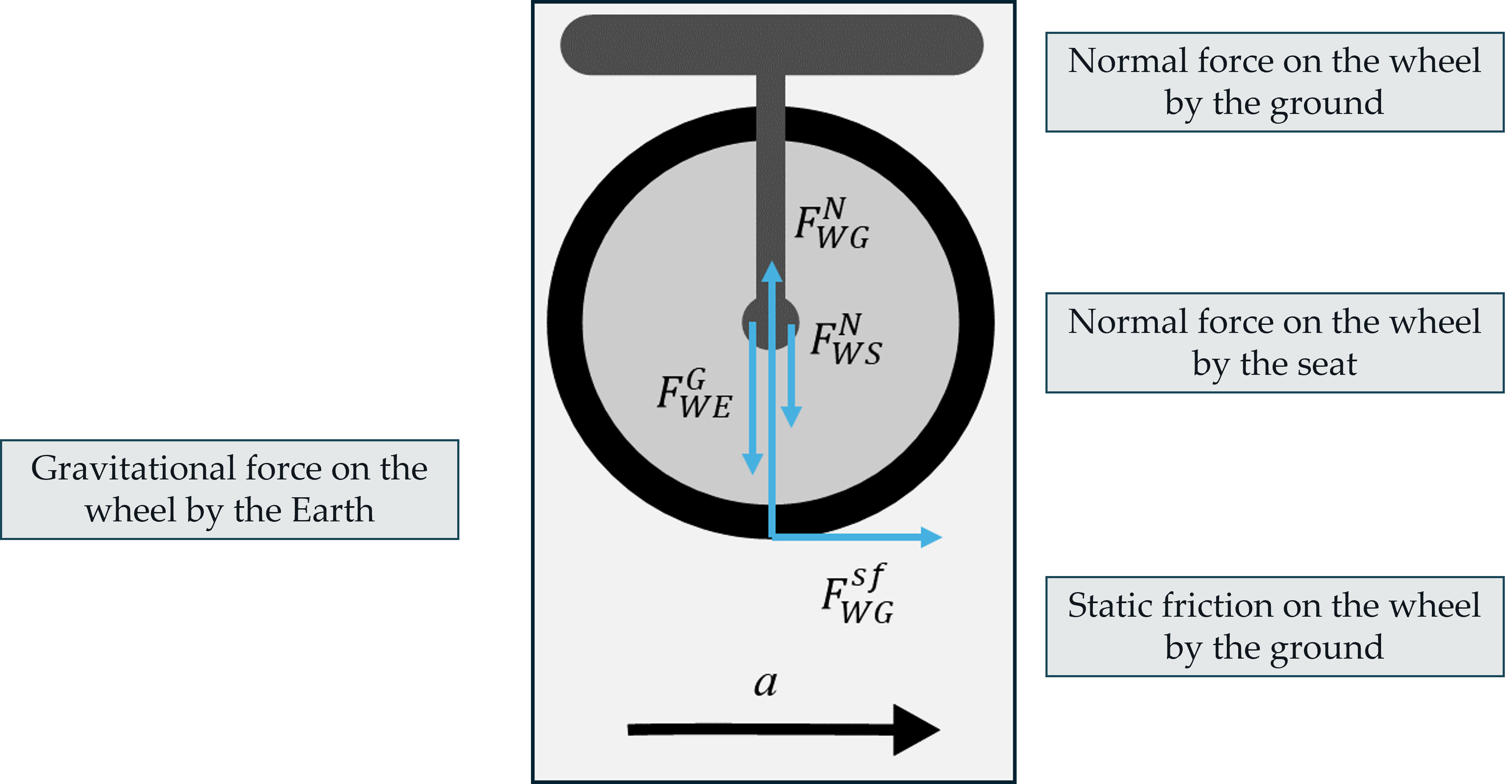
Activity 12.8.1. The Unicycle.

Shown below is a unicycle (a vehicle with one wheel), which has mass \(m\text{,}\) radius \(R\text{,}\) and axle radius \(r\) that is accelerating to the right.
Figure 12.8.1. Two ropes connected to a board that is free to rotate

(a)

How is the tire’s angular acceleration \(\alpha\) related to the tire’s translational acceleration \(a_t\text{?}\)
Answer.
\begin{equation*} \alpha=\frac{a_t}{R} \end{equation*}

(b)

Draw an extended free-body diagram for the wheel.
Tip.
Figure 12.8.2. A possible free-body diagram showing four forces acting on the wheel.

(c)

What direction is the net force on the unicycle?
Answer.
To the right

(d)

What direction must the net torque on the unicycle be to get the wheel spinning?
Answer.
Into the page
Solution.
The angular acceleration is clockwise, to get the wheel spinning, so the net torque must be in that same direction.

(e)

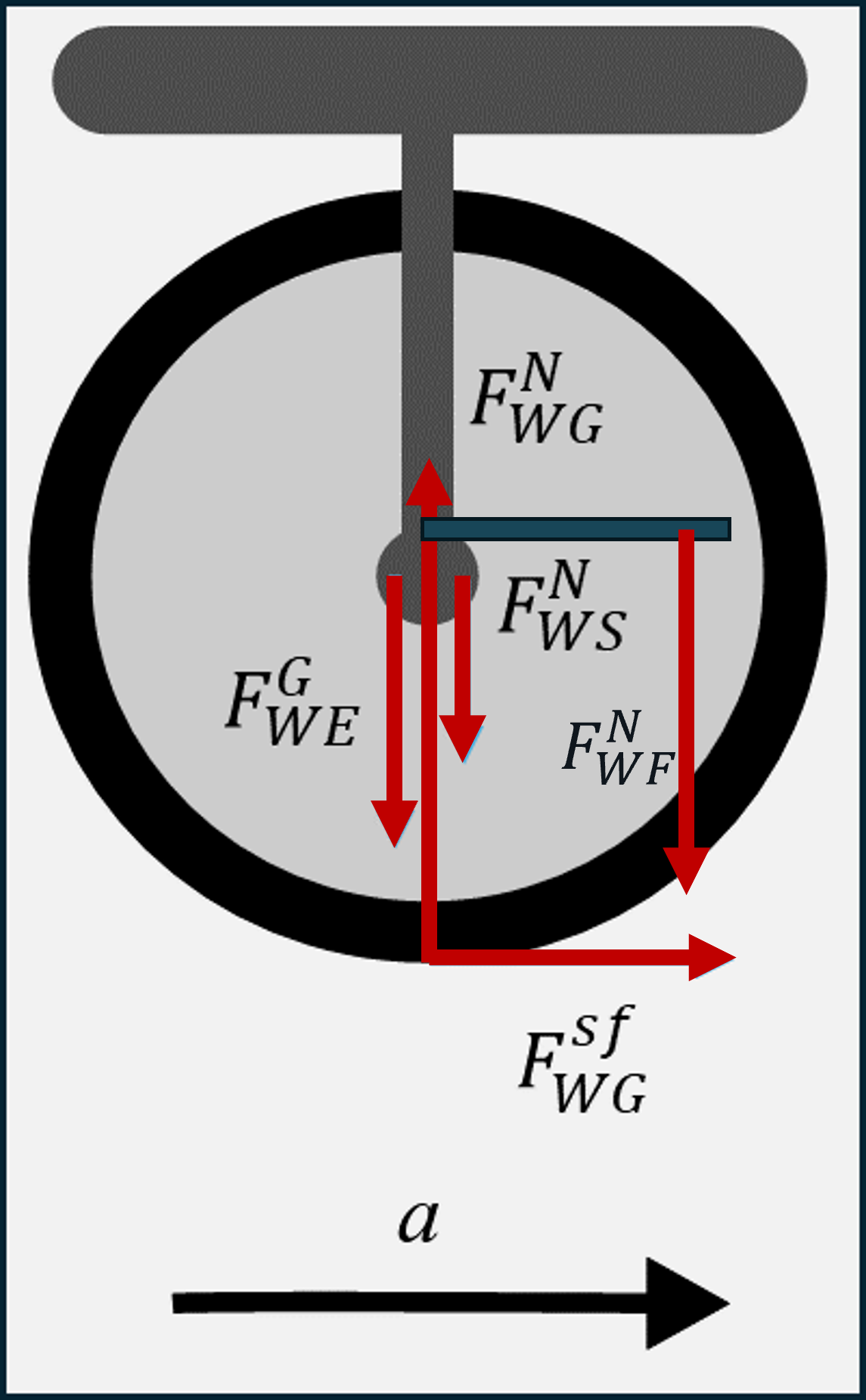
In the tip above is an Incorrect Free-body Diagram for the Unicycle Wheel. Show that the net torque about the center of the wheel is not consistent with the angular acceleration of thew heel. How would you modify that free-body diagram so that the net torque is consistent with the angular acceleration?
Answer.
Figure 12.8.3. A free-body diagram showing five forces acting on the wheel.
Solution.
One resolution is to add a pedal. By adding a pedal to the wheel, you can then add a normal force on the wheel by a foot, so that pushing down on the pedal would provide a clockwise torque.
Another option is for the person riding the unicycle to lean forward. This would also provide the clockwise torque needed to accelerate. A real unicycle rider will typically lean forward and have a pedal.

A*R*C*S 12.8.2. Leaning Forward on a Unicycle.

A person of mass \(M\) is riding a unicycle of mass \(m\text{.}\) They want to accelerate forward at a rate \(a\text{.}\) How far forward must the person lean in order to achieve this?
Tip.
Write down both the Law of Motion and the Rotational Law of Motion!
Solution.
Figure 12.8.4. A free-body diagram for the unicycle.
The Law of Motion says:
\begin{equation*} F^{sf} = (m + M)a \end{equation*}
Both the wheel and the person are accelerating forward.
The Rotational Law of Motion says:
\begin{equation*} F_{WS}^N d - F^{sf} R = mR^2\frac{a}{R} \end{equation*}
\begin{equation*} Mgd - R(m + M)a = mRa \end{equation*}
\begin{equation*} d = \frac{(2m + M)}{M}\frac{a}{g}R \end{equation*}
Covariational Reasoning: If the acceleration increases, the distance you lean forward must increases. If you want to accelerate more, the tires need to spin faster, which means a higher angular acceleration, which requires more torque. By leaning forward more, more torque is applied to the wheel.
If the mass of the wheel increases, you must lean forward more. This is because by increasing the mass of the wheel, the moment of inertia increases, so to angularly accelerate at the same rate, more torque is needed.
PrevTopNext