1. Sensemaking: Units.
Explicitly check the units of \(\nu_{\text{sound}} \) to confirm its relationship holds.
Section 7.8 Sound Waves
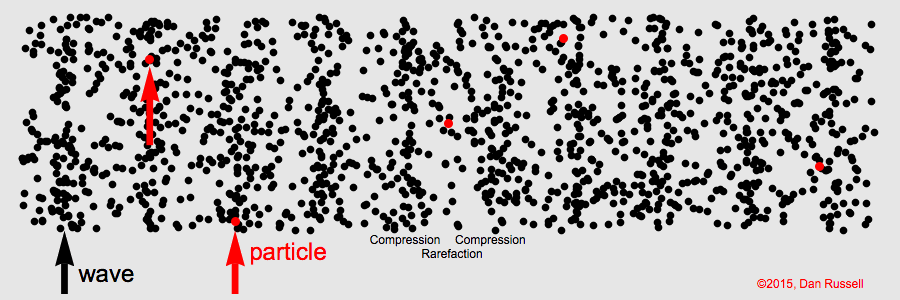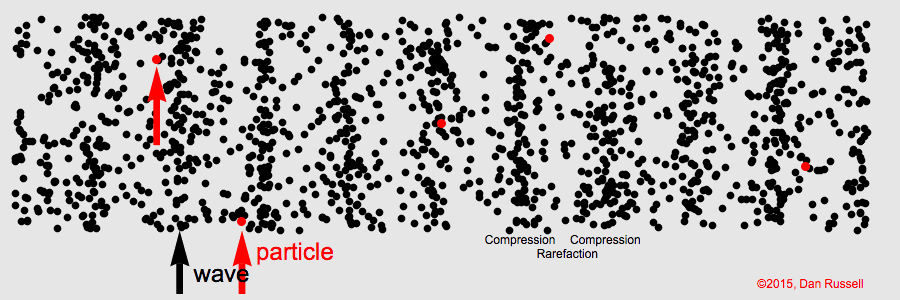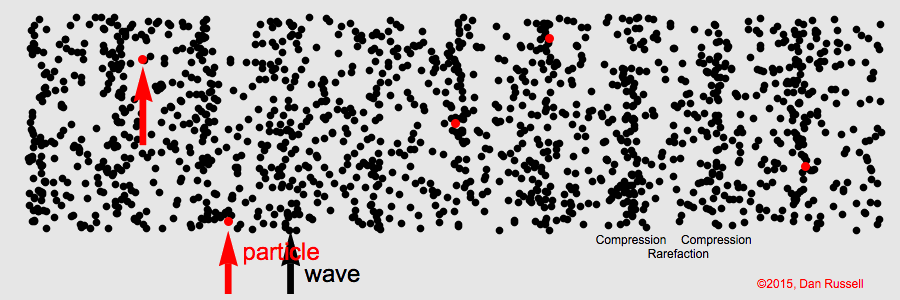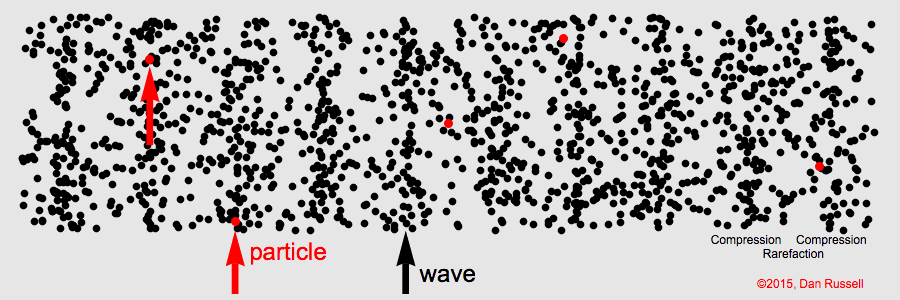
A sound wave is a sequence of compressions where the density is greater than the average and rarefactions where the density is below the average density in the substance. The substance can be air, water, solid, or plasma.
Consider a substance that has density \(\rho \text{.}\) The wave disturbance travels outward from the source of the wave through the substance at the wave speed \(\nu \) which depends on the compressibility of that substance. A substance’s compressibility is characterized by its bulk modulus \(B \text{.}\) The SI units of bulk modulus are the units of pressure, Pascals (Pa). If pressure \(P \) is applied to a substance of volume \(V \) then the fraction by which it is compressed is
\begin{equation*}
\frac{\Delta V}{V}= - \frac{P}{B}
\end{equation*}
where the negative sign tells us that the volume decreases as the substance is compressed. You can predict the speed of sound in a substance, which is the speed at which the compression wave travels
\begin{equation*}
\nu_{\text{sound}} = \sqrt{\frac{B}{\rho}}
\end{equation*}
At \(0^{\circ} C\) and 1.0 atmosphere standard pressure, the density of air is \(\rho_0 = 1.292 \frac{\text{kg}}{\text{m}^3} \) and the bulk modulus is \(B_0=1.48 x 10^5 \text{ Pa}\text{.}\) Thus the speed of sound in air is
\begin{equation*}
\nu_{\text{sound}} = \sqrt{\frac{B_0}{\rho_0}}=331 \text{m/s}
\end{equation*}
You can use the ideal gas law to show that density at constant pressure is inversely proportional to the temperature \(T \) measured in Kelvin. Therefore the speed of sound in air at 1.0 atmosphere standard pressure is
\begin{equation*}
\nu_{\text{sound}}(T) = \sqrt{\frac{B_0}{\rho_0}\frac{T}{273}} = 331 \frac{\text{m}}{\text{s}} \sqrt{\frac{T}{273}}
\end{equation*}
Exercises Activities
2. Sensemaking: Numbers.
A commonly cited value for the speed of sound is 343 m/s. What is the temperature corresponding to this speed? Why do you think this number is commonly cited?
References References
[1]
Animations courtesy of Dr. Dan Russell, Grad. Prog. Acoustics, Penn State. licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. For more information see
https://www.acs.psu.edu/drussell/demos.html
