Section 11.3 Centripetal Acceleration
Recall your predictions from Applying Physics Models and compare them to the solutions in the video below.
Subsubsection Key Ideas
When an object moves along a curved path, the instantaneous velocity always points tangent to the curve.
Exercises Model Application - Acceleration Direction
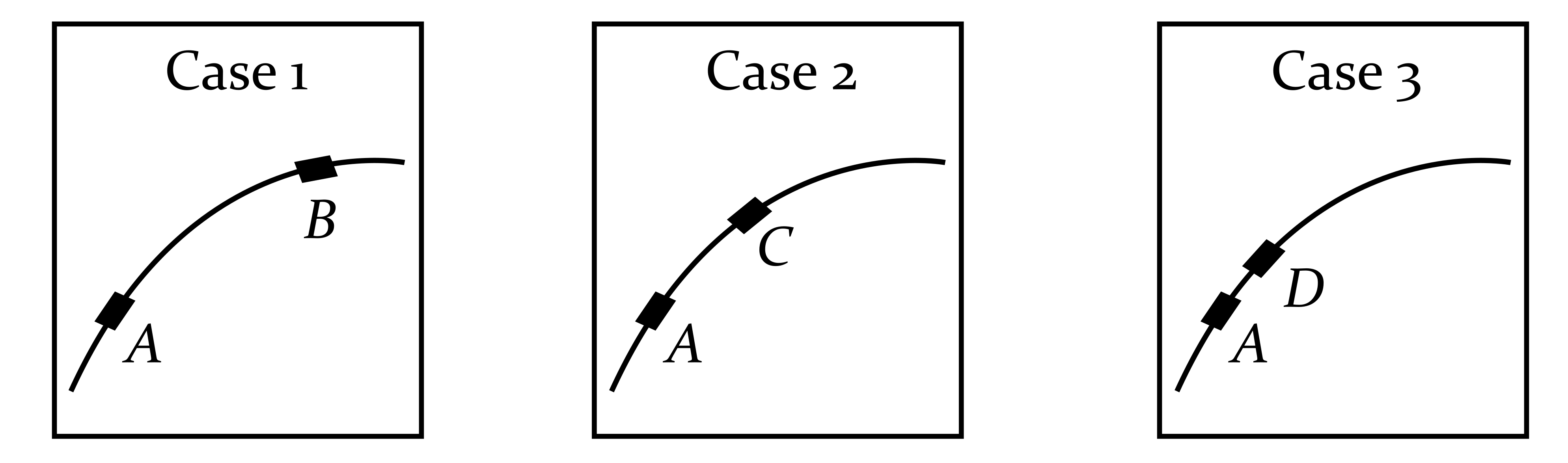
The figure below shows four different instants (A-D) for a car moving clockwise along a curved path at constant speed.
1.
Sketch vectors for the instantaneous velocity at each instant.
2.
Sketch vectors for the change in velocity for each case.
3.
Use the definition of instantaneous acceleration to determine the direction of the car’s acceleration at instant A.
Video Lesson 11.3.3. Centripetal Acceleration Direction.
Exercises Model Application - Acceleration Magnitude
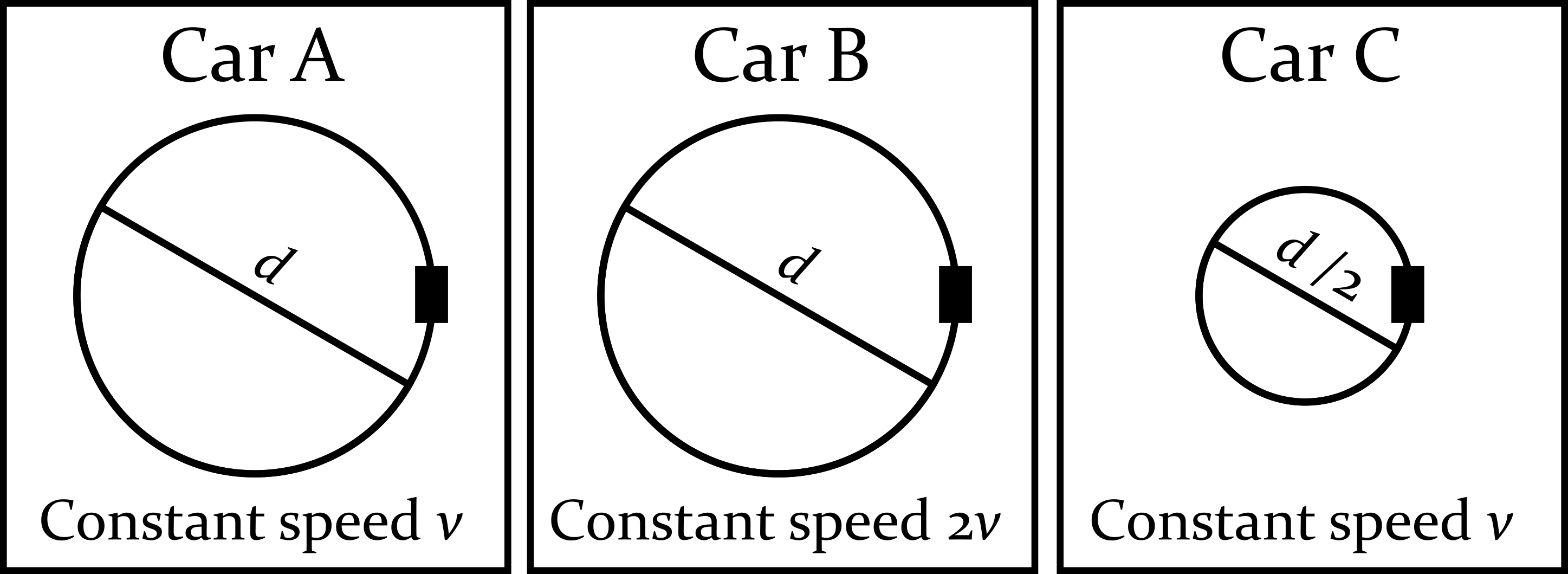
The figure below shows three identical cars, each moving around a circular track. Cars A and B move at different constant speeds around tracks with the same radius. Cars A and C move at the same speed around tracks with different radii.
1.
Predict which of the three cars has an acceleration with the largest magnitude. Explain your reasoning
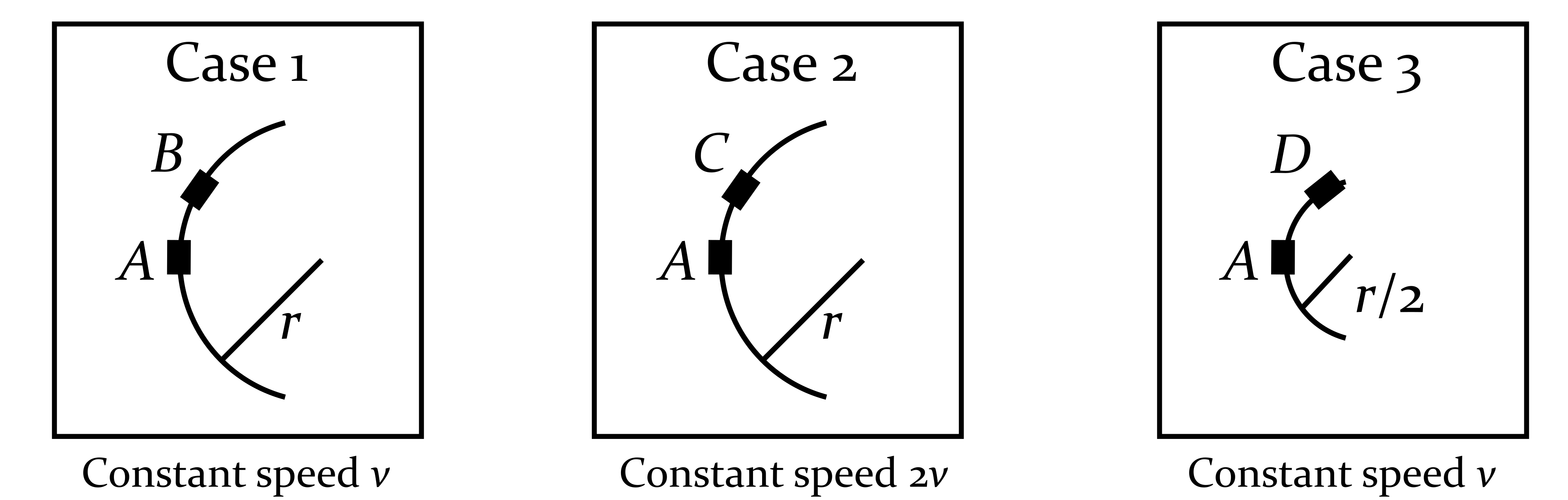
The figure below shows several instants for the cars described above. In each case, the two points are separated by the same distance along the path.
2.
Sketch vectors for the instantaneous velocity for each point.
3.
Sketch vectors for the change in velocity for each case.
4.
Use the definition of instantaneous acceleration to rank the magnitudes of the cars’ accelerations.
Video Lesson 11.3.6. Centripetal Acceleration Magnitude.
Definition 11.3.7. Centripetal Acceleration.
An object moving along a curved path experiences a centripetal acceleration that points perpendicular to the path (inward) with magnitude \(a_{c} = \frac{v^2}{r}\text{,}\) where \(r\) is the local radius of curvature. If the object is moving at constant speed, the acceleration is entirely centripetal.
