Skip to main content

Learning Introductory Physics with Activities

Paul J. Emigh, Rebecka Tumblin, Kathryn Hadley, Danielle Skinner

Section 5.5 Using Action-Reaction Pairs

Exercises Practice Activities

🔗

Activity 5.5.1. The Book Stack.

A stack of two books is at rest on a table.
🔗
Figure 5.5.1. A stack of two books.
🔗
Use Force Analysis to identify all Action-Reaction (Newton’s 3rd Law) Pairs and identify any forces that are equal in magnitude.
🔗
🔗

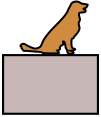
Activity 5.5.2. A*R*C*S: Uh-Oh Dr. Paws.

The instructor pushes a footstool (mass \(m_1\)) across the floor with a constant force so that the footstool speeds up. Dr. Paws (a dog with mass \(m_2\)) is sitting on the footstool. The coefficient of static friction between the dog and footstool is \(\mu\) (assume no friction with the ground).
🔗
Figure 5.5.2. A simplified sketch of a dog on a footstool.
🔗

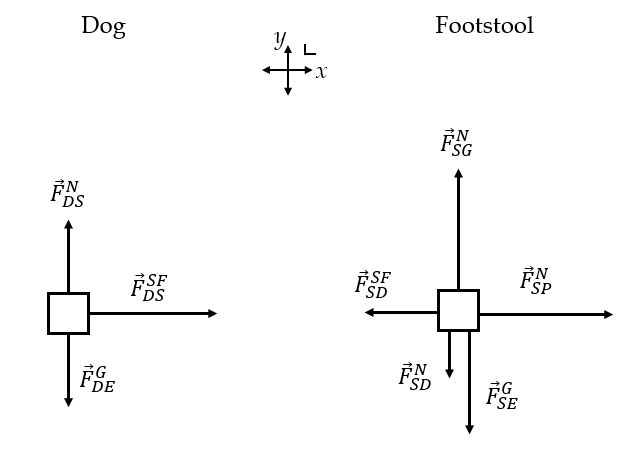
(a) 1. Analyze and Represent.

In the example that follows, describe why the assumptions are reasonable, identify all Action-Reaction (Newton’s 3rd Law) Pairs, and identify and fix the problems with the free-body diagrams.
🔗
  1. List quantities.
    🔗
    Mass of the footstool: \(m_1 = 10 \mathrm{~kg}\)
    🔗
    Mass of the dog: \(m_2 = 30 \mathrm{~kg}\)
    🔗
    Coefficient of static friction: \(\mu = 0.4\)
    🔗
    Instructor force: \(F_i = ?\)
    🔗
    🔗
  2. Identify assumptions.
    🔗
    Near-earth: \(g = 10 \mathrm{~m/s^2}\text{;}\) particle-model; neglect air-resistance; no friction with the ground.
    🔗
    🔗
  3. Represent the situation physically.
    🔗
    🔗
Figure 5.5.3. Two free-body diagrams.
🔗
🔗
🔗

(b) 3. Sensemake.

You have three friends who each calculate a different equation for the maximum allowable force the instructor can apply:
\begin{equation*} F_{SP}^N = \mu \frac{𝑚_1}{𝑚_1 + 𝑚_2}g \end{equation*}
\begin{equation*} F_{SP}^N = \mu\left( 𝑚_2 - 𝑚_1 \right)g \end{equation*}
\begin{equation*} F_{SP}^N = \mu \frac{𝑚_1 𝑚_2}{(𝑚_1 + 𝑚_2}g \end{equation*}
Use a sensemaking strategy to give a reason why each expression is incorrect.
🔗
🔗

(c) 2. Calculate.

  1. Represent physics principles that will help you solve for the tension and the acceleration.
    🔗
    🔗
  2. Determine a symbolic equation for each unknown quantity in terms of known variables.
    🔗
    🔗
  3. Plug numbers into your symbolic answer.
    🔗
    🔗
🔗
🔗
🔗

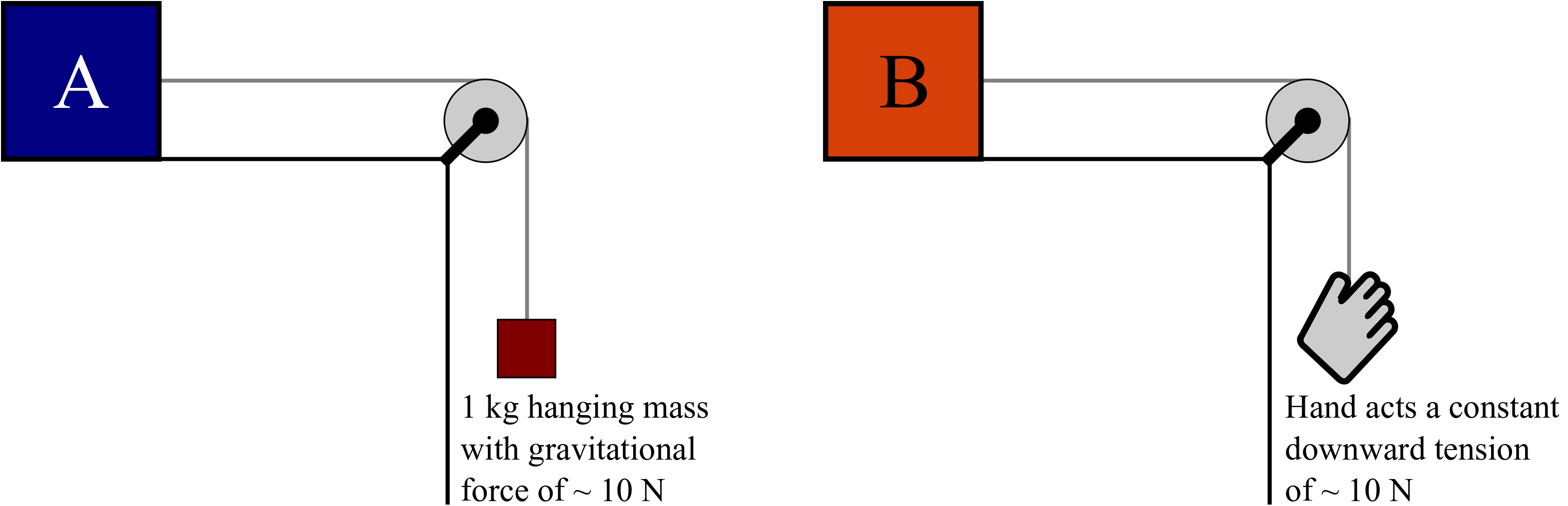
Activity 5.5.3. The Block Race.

Block A is accelerated across a frictionless table by a hanging \(10 \mathrm{~N}\) mass. An identical block B is accelerated by a constant \(10 \mathrm{~N}\) tension in the string.
🔗
Figure 5.5.4. Two Blocks connected to strings.
🔗

(a)

Before you begin, predict which block you think will have a larger acceleration.
🔗
🔗

(b)

Use Force Analysis to determine the acceleration of each block. Sketching free-body diagrams for each object is essential!
🔗
🔗
🔗

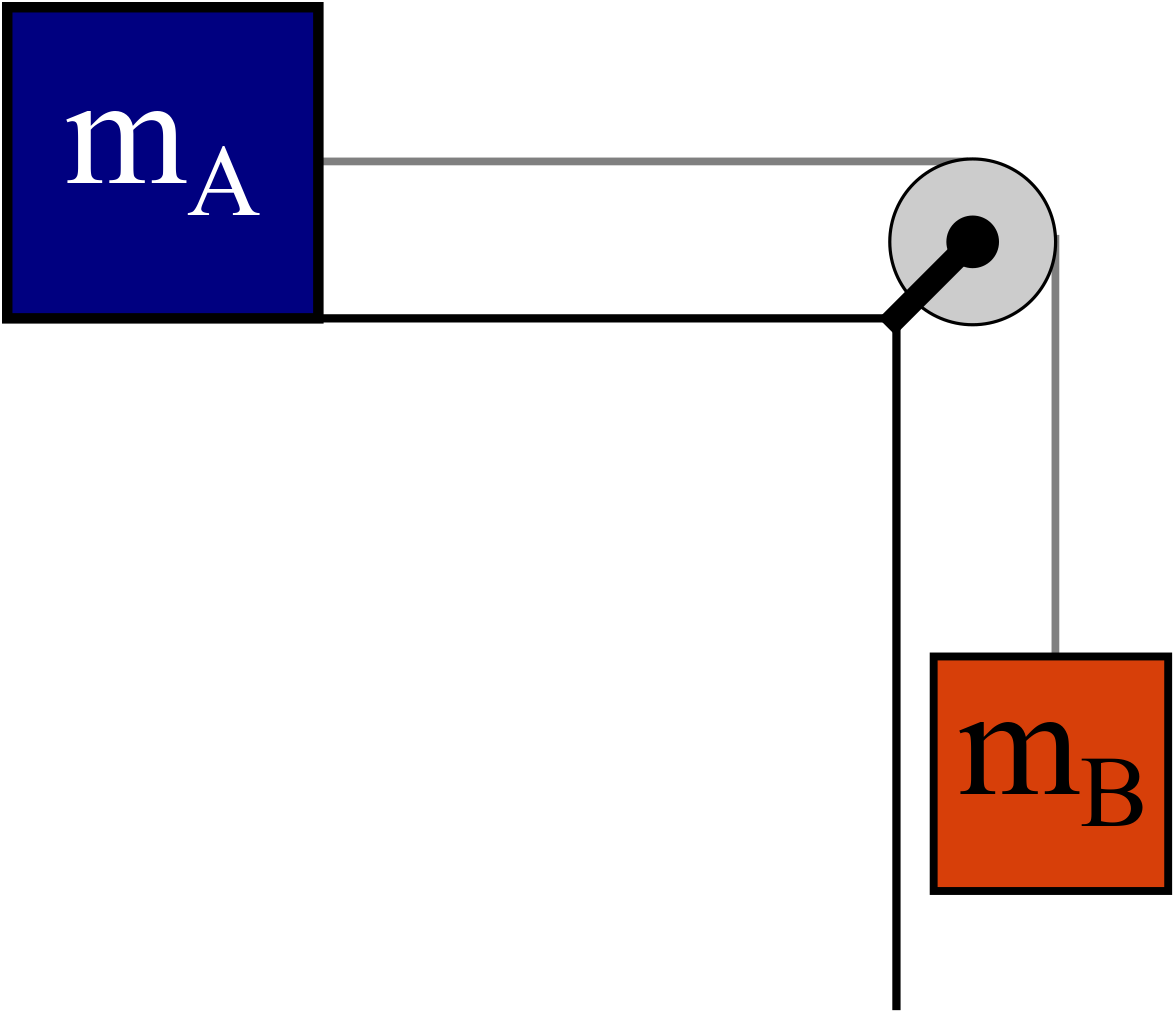
Activity 5.5.4. The Pair of Blocks.

Blocks A and B are connected by an ideal string via a massless pulley. The coefficient of kinetic friction is \(\mu\text{.}\)
🔗
Figure 5.5.5. Two Blocks connected by a string over a pulley.
🔗
Use the A*R*C*S Steps to determine the acceleration of each block.
🔗
This situation is a particularly good one for special-case analysis: what are some cases you might want to try?
🔗
🔗

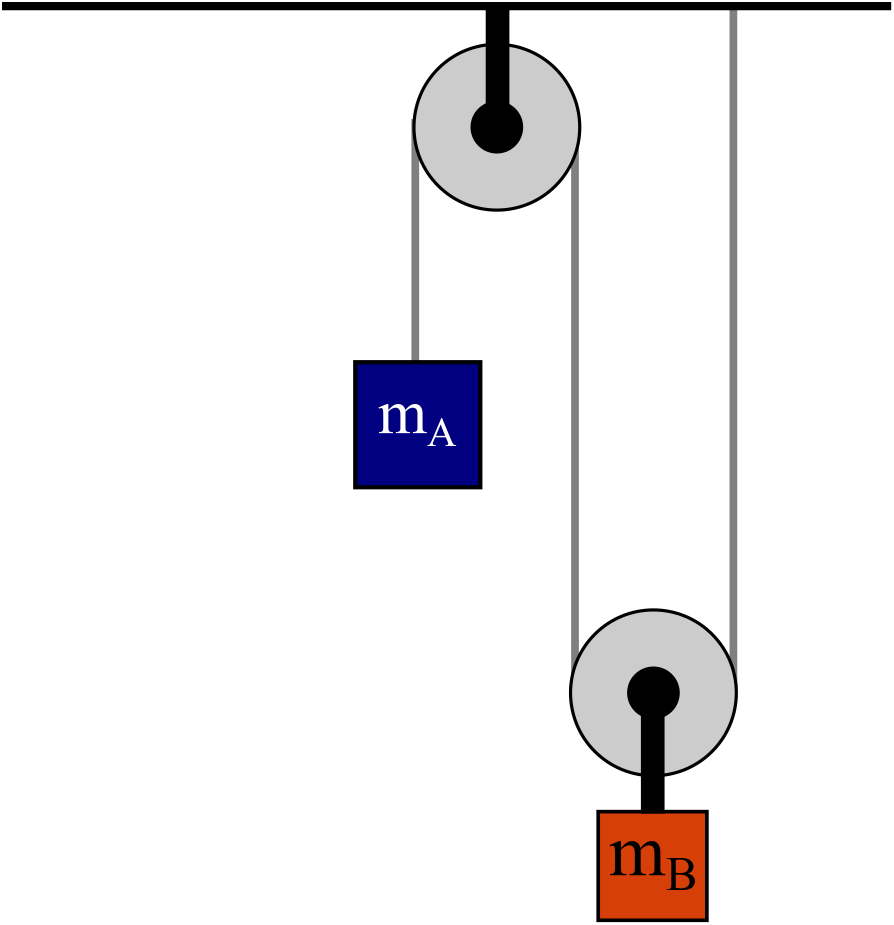
Activity 5.5.5. The Pair of Pulleys.

Blocks A and B are connected by an ideal string via two massless pulleys.
🔗
Figure 5.5.6. Two Blocks connected by a string to two pulleys.
🔗
Use the A*R*C*S Steps to determine the acceleration of each block.
🔗
Tip.
The magnitudes of the block’s accelerations are different. How can you relate them?
🔗
🔗
🔗
🔗
PrevTopNext