Skip to main content

Learning Introductory Physics with Activities

Paul J. Emigh, Rebecka Tumblin, Kathryn Hadley, Danielle Skinner

Section 2.4 Displacement

Definition 2.4.1. Displacement.

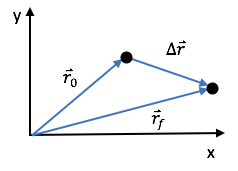
The displacement of an object describes the change in that object’s position: \(\Delta \vec{r} = \vec{r}_f - \vec{r}_i\text{.}\) If the displacement is infinitesimal, you would write \(\vec{dr}\) instead of \(\Delta \vec{r}\)
Suppose an object is initially located at position \(\vec{r}_0\) at some initial time \(t_0\) and the object is moving through space over an interval of time \(\Delta t = t_f - t_0\text{.}\) The symbol \(\Delta\) (the capital Greek letter "Delta") represents a change in a quantity.  The time interval \(\Delta t\) measures the elapsed time as the object moves from an initial position \(\vec{r}_0\)  at initial time \(t_0\) to a final position \(\vec{r}_0\) and some final time \(t_f\text{.}\) The vector \(\Delta \vec{r}\) is called the displacement of the object over the time interval \(\Delta t\text{.}\) Here, the subscript 0 refers to some initial time: in some cases, the subscript \(o\) ("naught") or \(i\) (for "initial") is used instead of 0.

Note 2.4.2. Subscripts.

You have probably noticed that physics notation uses subscripts to mean a lot of different things! In general, physics symbols try to be descriptive, choosing evocative letters like \(m\) for mass and \(t\) for time. Physics symbols also try to be specific (\(m_1\) for the mass of object 1, \(m_2\) for the mass of object 2, etc.) and detailed (\(t_i\) for the initial time and \(t_f\) for the final time). Sometimes, subcripts might even be combined: \(r_{x3i}\) for the \(x\)-component of object 3’s initial position. As you practice, you will start to get a sense for all the different things you can use a subscript for.
On an xy axis, two arrows labeled r0 and rf point up and to the right, with a third vector labeled Delta r completing a triangle between them.
Figure 2.4.3. A displacement vector.

Exercises Activities

1. Practice: Vectors in the Park.

You and your friend are each standing at opposite ends of a \(125 \mathrm{~m}\) long park. Your friend, who is initially due south of you, walks \(50 \mathrm{~m}\) east and stops to wait for you. Then, you walk in a straight line until you reach your friend.
  1. Choose an origin of coordinates for this problem and make a sketch of the context.
  2. Write initial and final position vectors for both you and your friend.
  3. Find the displacement vector for both you and your friend.
  4. Reflect on your choice of origin for this problem. What impact did your choice have on how you solved it? Could you have made a different choice?
PrevTopNext