Skip to main content

Learning Introductory Physics with Activities

Paul J. Emigh, Rebecka Tumblin, Kathryn Hadley, Danielle Skinner

Section 13.8 Application: Moment of Inertia for a Ring

Activity 13.8.1. Warm-up: The Moons of Mars.

Mars has two moons, Phobos and Deimos, which have the following orbital properties:
\begin{equation*} R_p = 9 \times 10^6 \mathrm{~m} \end{equation*}
\begin{equation*} R_d = 20 \times 10^6 \mathrm{~m} \end{equation*}
\begin{equation*} M_p = 11 \times 10^15 \mathrm{~kg} \end{equation*}
\begin{equation*} M_d = 2 \times 10^15 \mathrm{~kg} \end{equation*}
  1. Sketch a diagram showing Mars, Phobos, and Deimos.
  2. Find the moment of inertia of each moon (on it’s own) about an axis passing through Mars
  3. Find the moment of inertia for the system consisting of the two moons about an axis passing through Mars

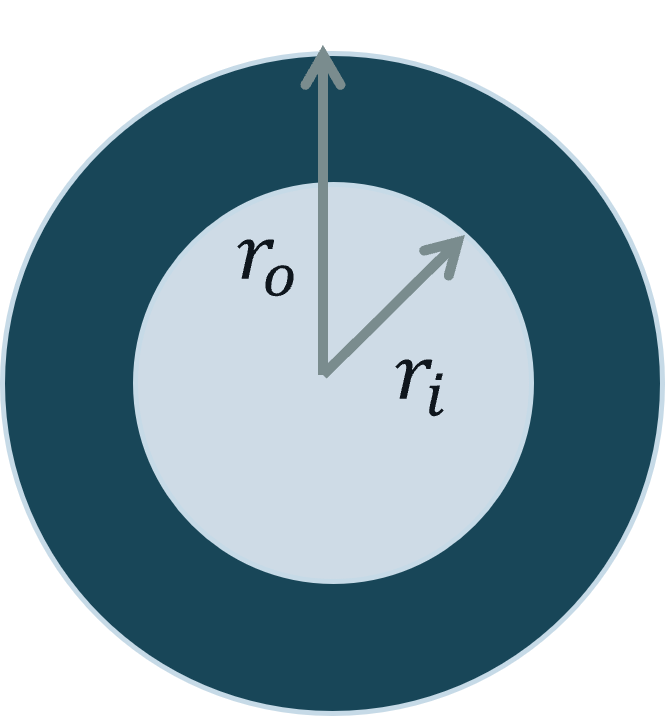
Activity 13.8.2. The Ring.

The ring shown below has mass \(m\text{,}\) inner radius \(r_i\text{,}\) and outer radius \(r_o\text{.}\) Calculate the moment of inertia about an axis through the center, perpendicular to the screen.
Figure 13.8.1. A ball suspended from the ceiling by a string.

(a)

Explain why the mass density can be given by:
\begin{equation*} \sigma = \frac{m}{\pi(r_o^2 - r_i^2)} \end{equation*}

(b)

Chop: How would you chop the ring up into small pieces? Draw a diagram showing the small pieces and label \(dm\text{,}\) \(dA\text{,}\) and \(r\text{.}\) Find the mass of one of the small pieces you drew.

(c)

Multiply: Using the results from the previous steps, multiply the components together to get your infinitesimal \(dl\text{.}\)

(d)

Add: Compute the integral for the moment of inertia.

(e)

Use special-case analysis in the limit that \(r_i\) approaches \(r_o\) to make sense of your answer.

(f)

Use the parallel axis theorem to find the moment of inertia of the ring about an axis passing through its outer edge (perpendicular to the ring).

(g)

Use an integral to verify the center of mass of the ring.
PrevTopNext