Section 18.6 Single-Slit Diffraction
Single-slit diffraction is an interesting case where we still see interference of light, even when there is only one single slit, because of the assumptions made in Huygen’s Principle.
Subsubsection Key Ideas
Principle 18.6.2. Single-Slit Diffraction.
The location of dark spots due to light shining through a single slit on a distant screen can be determined by \(a \sin\theta = p \lambda\) for \(p = 1, 2, 3, ...\text{.}\)
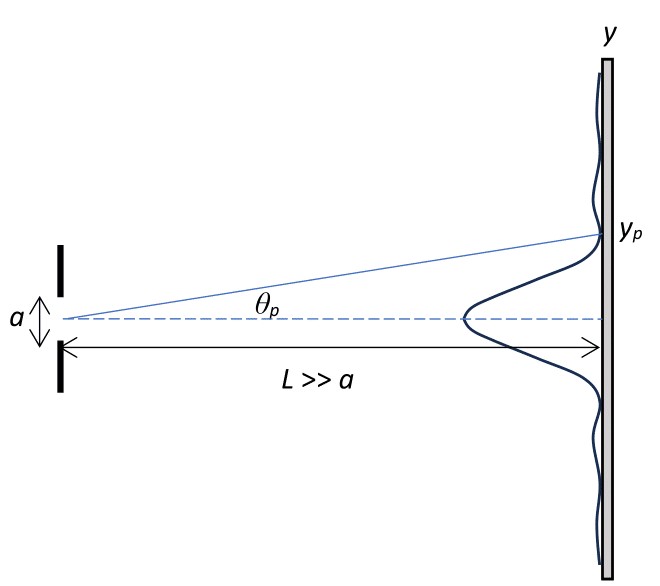
Subsubsection Single-Slit Diffraction Activities
Activity 18.6.1. Comparing Interference and Diffraction.
What differences do you notice between the single-slit diffraction pattern on the screen and the double-slit interference patterns you have seen previously?
Activity 18.6.2. Single-Slit Diffraction Simulation.
Play with the
light interference simulation for a few minutes. Click on the “Diffraction” tab.
Write down some observations. Play with different opening shapes. For the square shape, what happens when you change the width? What happens to the image as you change the frequency of the light?
Activity 18.6.3. Width of a Diffraction Pattern.
The width of the central bright maxima in a single-slit diffraction pattern can be measured by looking at the distance to the first dark spot. What happens to the width as the distance between the slit and the screen increases? What happens to the width as the wavelength decreases? What happens as the slit size decreases?
