Skip to main content

Learning Introductory Physics with Activities

Paul J. Emigh, Rebecka Tumblin, Kathryn Hadley, Danielle Skinner

Section 18.4 Many-slit Interference

In the previous section, you built a model for what happens when light is incident on two very narrow slits. As more and more slits are added, the interference pattern and the intensity of the light is altered.
🔗

Exercises Many-slit Interference

To understand how the interference pattern changes, let’s work through what happens if you add a third slit to the screen. Let’s consider three points on the screen: the central maximum, the first bright spot, and the first dark spot.
🔗
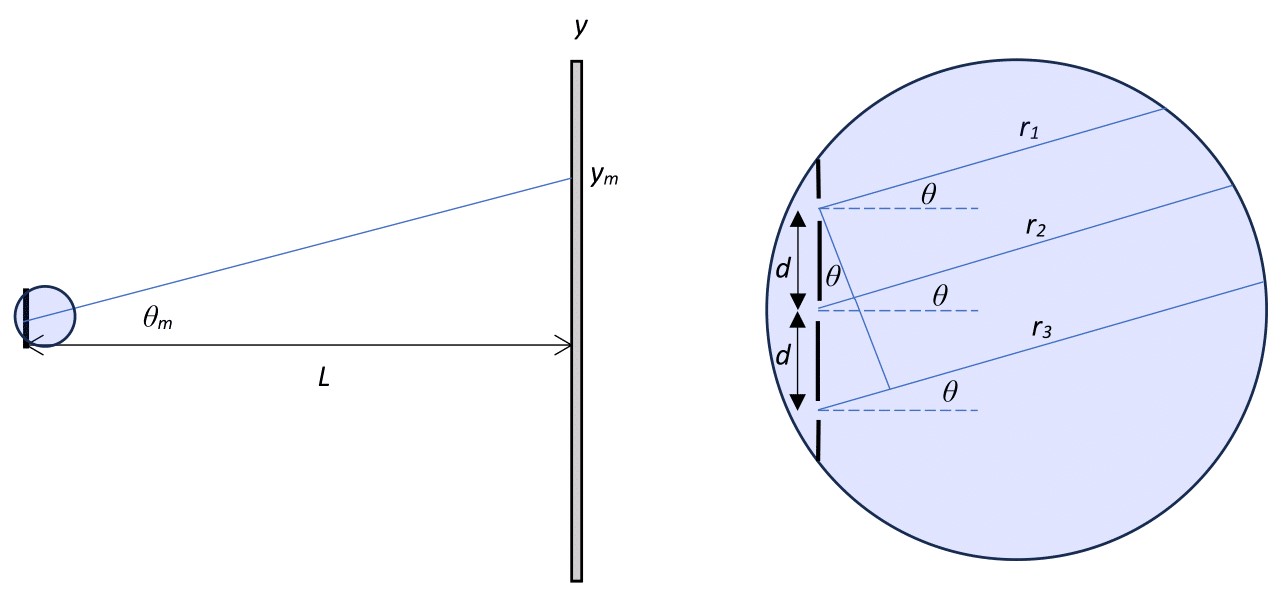
On the left side, there is a diagram of the triple-slit experiment, with the slits sitting on the left a distance L away from a screen. A dashed line extends from the center of the slits to the screen at an angle theta sub m and hits a point y sub m on the screen on the right. A small circle covers the triple-slit experiment on the right. On the right side, there is a zoomed-in picture of the triple-slit set up inside a circle. Three slits sit at a distance d away from each other. A ray extends from each slit to the right side of the circle at an angle theta. The rays are labelled "r 1", "r 2", and "r 3". Another line extends from the top slit to the bottom ray at an angle theta, indicating the path length difference.
Figure 18.4.1. Left: A diagram of the triple-slit experiment. Three slits are located in the center of a plane located a distance \(L\) away from a screen. Right: A zoomed-in view of the circle on the left. Notice how a third slit has been added below the second slit, also at a distance \(d\) away from the second slit.
🔗

1. Central Maximum.

First consider the central maximum.
🔗
  1. What is the path length difference between ray \(r_1\) and \(r_2\text{?}\)
    🔗
  2. What is the path length difference between ray \(r_2\) and \(r_3\text{?}\)
    🔗
  3. What is the path length difference between ray \(r_1\) and \(r_3\text{?}\)
    🔗
  4. Is this a point of constructive or destructive interference?
    🔗
  5. How does this affect the intensity of the light?
    🔗
Answer.
The path length difference between all three rays is zero. The reason for this is because the central maximum lies at the center of the screen at an angle of \(\theta = 0\text{.}\) Therefore, the path length difference is zero. This means that the central maximum will be a point of constructive interference. With the added light coming from the third slit, the intensity of the central maximum increases.
🔗
🔗
🔗

2. First Bright Spot.

Now look at the second bright spot.
🔗
  1. What is the path length difference between ray \(r_1\) and \(r_2\text{?}\)
    🔗
  2. What is the path length difference between ray \(r_2\) and \(r_3\text{?}\)
    🔗
  3. What is the path length difference between ray \(r_1\) and \(r_3\text{?}\)
    🔗
  4. Is this a point of constructive or destructive interference?
    🔗
  5. How does this affect the intensity of the light?
    🔗
Answer.
The path length difference between rays \(r_1\) and \(r_2\) and the difference between rays \(r_2\) and \(r_3\) is \(\lambda\text{.}\) The path length difference between \(r_1\) and \(r_3\) is \(2\lambda\text{!}\) So this is also a point of constructive interference. With the added light coming from the third slit, the intensity of the first bright spot increases.
🔗
🔗
🔗

3. First Dark Spot.

Finally, consider the first dark spot.
🔗
  1. What is the path length difference between ray \(r_1\) and \(r_2\text{?}\)
    🔗
  2. What is the path length difference between ray \(r_2\) and \(r_3\text{?}\)
    🔗
  3. What is the path length difference between ray \(r_1\) and \(r_3\text{?}\)
    🔗
  4. Is this a point of constructive or destructive interference?
    🔗
  5. How does this affect the intensity of the light?
    🔗
Answer.
The path length difference between rays \(r_1\) and \(r_2\) and between rays \(r_2\) and \(r_3\) is \(\lambda / 2\text{.}\) The path length difference between \(r_1\) and \(r_3\) is \(\lambda\text{!}\) This means that while rays \(r_1\) and \(r_2\) and rays \(r_2\) and \(r_3\) are destructively interfering, rays \(r_1\) and \(r_3\) constructively interfering! The intensity at this point is no longer zero, as now there is some contribution of light coming from the third slit.
🔗
🔗
🔗
🔗
As you add more and more slits, spots that were bright in the two-slit experiment will only become brighter, and dark spots will no longer be completely dark.
🔗
🔗
PrevTopNext