You manage parks for Corvallis, and you are responsible for putting up fences around two new parks that have the same area. Park 1 is a square, while park 2 is a rectangle whose length is \(110 \mathrm{~m}\text{.}\) If park 2 requires twice as much fencing as park 1, what is the area of each park?
1. Analyze and Represent
- List quantities. The only known here is \(l = 110 \mathrm{~m}\text{,}\) the length of the rectangular park. There are many unknowns: \(s\) (the side length of the square park), \(w\) (the width of the rectangle), \(P_{square}\text{,}\) \(A_{rectangle}\text{,}\) and \(P_{rectangle}\text{,}\) and \(A_{square}\) (which we are trying to find).
- Identify assumptions. There is no physics in this activity, but the problem stated that the parks are rectangular, which is probably a simplification given that real parks are often strange shapes.
- Represent the situation physically. Below is a diagram of the square and the rectangle, with all distances labeled.
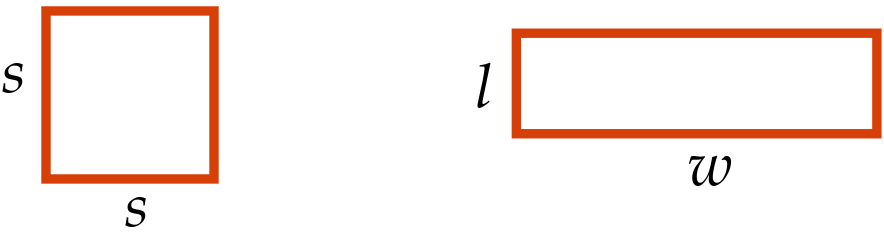
2. Calculate
- Represent principles symbolically. The area of a square is \(A_{square} = s^2\) and the perimeter (the length of the fence) is \(P_{square} = 4s\text{.}\) The area of a rectangle is \(A_{rectangle} = lw\) and the perimeter (the length of the fence) is \(P_{rectangle} = 2l + 2w\text{.}\)
- Solve unknown(s) symbolically. Start by setting the two areas equal and relating the perimeters\begin{equation*} A_{square} = A_{rectangle} \end{equation*}\begin{equation*} s^2 = lw \end{equation*}\begin{equation*} P_{rectangle} = 2P_{square} \end{equation*}\begin{equation*} 2l + 2w = 8s \end{equation*}Combine these expressions algebraically by solving the first equation for \(w\) and plugging it into the second equation:\begin{equation*} w = s^2/l \end{equation*}\begin{equation*} 2l + 2s^2/l = 8s \end{equation*}\begin{equation*} s^2 - 4sl + l^2 = 0 \end{equation*}Use the quadratic formula to solve this last equation for \(s\text{,}\) then square \(s\) to get the area of the square!\begin{equation*} s = \frac{4l \pm \sqrt{16l^2 - 4l^2}}{2} = \left(2 \pm \sqrt{3}\right)l \end{equation*}\begin{equation*} A = s^2 = \left(7 \pm 4\sqrt{3}\right)l^2 \end{equation*}
- Plug in numerical values. The two possible approximate values for \(A\) are \(13.9l^2 \approx 168190 \mathrm{~m^2}\) or \(0.07l^2 \approx 847 \mathrm{~m^2}\text{.}\)
3. Sensemake
- Are the units correct? The units for area should be \(\mathrm{m^2}\text{.}\) Each factor of \(l\) in our answer has units of \(\mathrm{m}\text{,}\) so squaring it gives \(\mathrm{m^2}\text{,}\) which is what we expect!
- Is your numerical answer reasonable? Something a little weird happened. You got two> numbers. What does that mean? In this case you were told that the length of the park was \(l\text{,}\) but you were not told whether the length was bigger or smaller than the width! The two cases correspond to those two possibilities. The units \(\mathrm{m^2}\) are not great for making sense of something as big as a park, so you can look up how many \(\mathrm{m^2}\) are in an acre (4047), which is a more reasonable measure of land area for a park. This gives us 41.6 acres (this would be a pretty big park!) and 0.2 acres (on the other hand, very small).
- Does your symbolic answer make physical sense? A quick way to check if our answer makes sense is to evaluate how it depends on the given quantities. In our case, the area varies like \(l^2\text{.}\) First of all, it depends on the square of \(l\text{,}\) which is something you have seen before in many other expressions for area, such as for squares, circles, polygons, etc. More specifically, this means that increasing \(l\) (making the given parameter bigger) corresponds to an increase in the area. Lastly, we can check special values of \(l\) and see what your answer is. The most special value of \(l\) is \(l = 0\text{,}\) which corresponds to no park at all! In this case, the area of the park should of course be 0, which is what your symbolic answer says as well:\begin{equation*} A = s^2 = \left(7 \pm 4\sqrt{3}\right) 0^2 = 0 \end{equation*}