Section 26.2 RC Charging Circuits
Exercises Activities
The circuit below contains a battery, a resistor, a switch, and a capacitor. The capacitor is initially uncharged and the voltage of the battery is \(V\text{.}\)
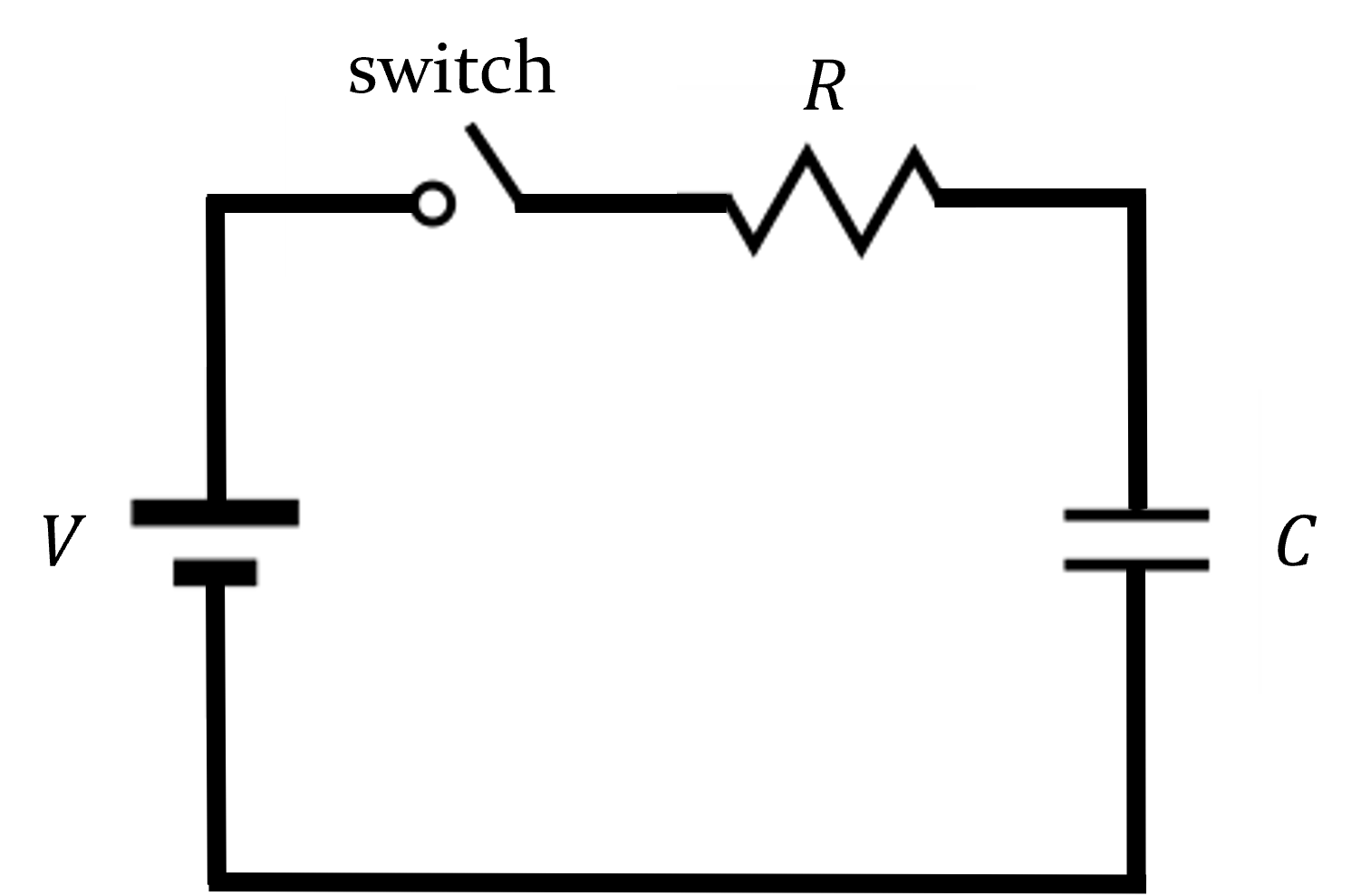
2.
Just after the switch is closed: what is the absolute value of the potential difference across the capacitor? Explain your reasoning.
3.
A long time after the switch is closed: what is the absolute value of the potential difference across the capacitor? Explain your reasoning.
When the capacitor is charging, the current through the resistor as a function of time is given by
\begin{equation*}
I(t) = \frac{V_{bat}}{R}e^{-t/RC}
\end{equation*}
4.
Given the result above, sketch a graph of the current through the resistor when the capacitor is charging. Describe how the graph would change if you were to increase the resistance of the circuit. Give a physical explanation for why you observe this change.
