Skip to main content

Learning Introductory Physics with Activities

Paul J. Emigh, Rebecka Tumblin, Kathryn Hadley, Danielle Skinner

Section 15.9 The Simple Pendulum

The figure below shows a simple pendulum: a small mass \(m\) at the end of a massless string of length \(L\text{.}\) The pendulum has an initial angular displacement from equilibrium \(\theta_i\) and is released from rest at \(t = 0\text{.}\)
🔗
Figure 15.9.1. A simple pendulum.
🔗

Exercises Simple Pendulum Activities

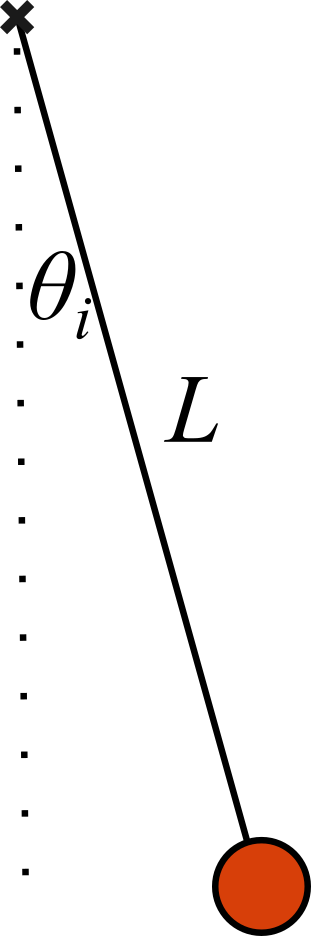
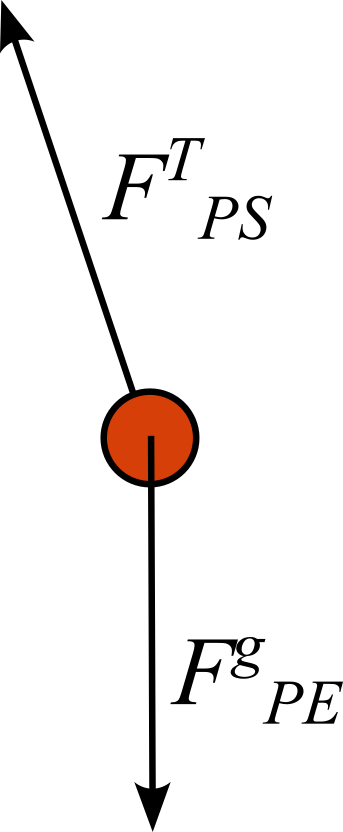
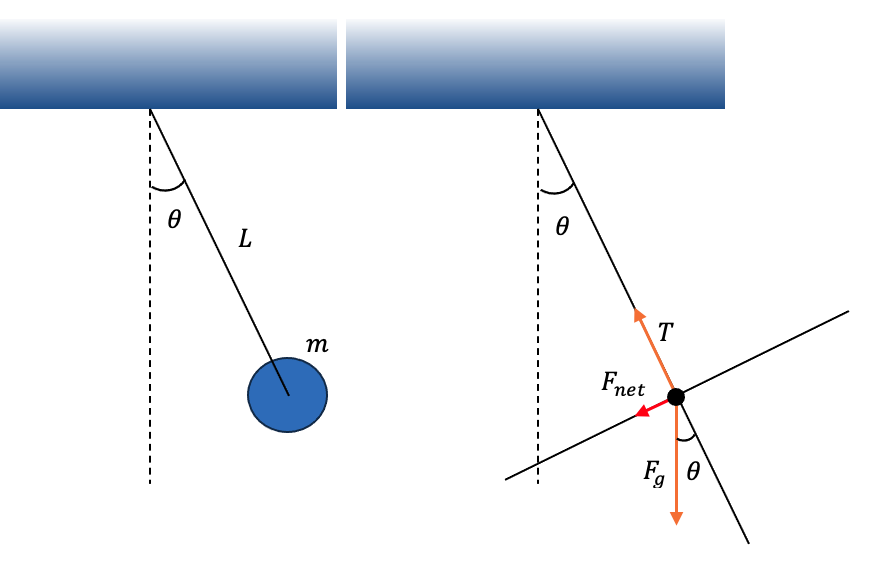
1. Finding Acceleration.

(a)
Sketch and label a Free-body diagram for the instant shown in the figure.
🔗
Solution.
Figure 15.9.2. A free-body diagram for a simple pendulum.
🔗
🔗
🔗
(b)
Determine the moment of inertia for the system of the pendulum about an axis of rotation through the top of the string (marked by \(\times\) in the figure).
🔗
Solution.
You can treat the pendulum as a point mass \(m\) a distance \(L\) from the axis of rotation, so \(I = mL^2\)
🔗
🔗
🔗
(c)
Determine the net torque on the pendulum about the top of the string (marked by \(\times\) in the figure).
🔗
Solution.
The tension force acts parallel to the string, so it acts a torque of zero on the pendulum. Gravity, however, acts at an angle to the string, so the torque is:
\begin{equation*} \tau = -mgL\sin\theta \end{equation*}
where the negative sign indicates that the torque is clockwise.
🔗
🔗
🔗
(d)
Use the Angular Law of Motion to solve for the angular acceleration
🔗
Solution.
\begin{equation*} \tau_{net} = I\alpha \end{equation*}
\begin{equation*} -mgL\sin\theta = mL^2\alpha \end{equation*}
\begin{equation*} \alpha = -\frac{g}{L}\sin\theta \end{equation*}
\begin{equation*} \frac{d^2}{dt^2}\theta = -\frac{g}{L}\sin\theta \end{equation*}
🔗
🔗
🔗
🔗

Note 15.9.3. Full Derivation of the Equation of Motion.

Consider a mass \(m\) that hangs from a string that has one end fixed in space and is free to pivot (i.e., no friction). Assume the string has negligible mass compared to the object’s mass \(m\) such that we can apply the massless string approximation to our analysis.
🔗
The string has length \(L \) and the mass is initially pulled out an angle \(\theta_{max}\) and then released. You know from experience that the pendulum will undergo oscillatory motion—what is the angular position as a function of time \(\theta(t)\) and the oscillation frequency \(\omega_p\) for the pendulum.
🔗
Figure 15.9.4. A pictorial representation of a simple pendulum and an accompanying free-body diagram.
🔗
Using torque analysis, first draw a pictorial representation of the situation and choose a coordinate system. Assume the mass can be treated as a particle and draw an extended free-body diagram, choosing an axis directed radially toward the pivot point and an axis tangential to the arc of the motion. Assume tension keeps the string taut so it does not bend or bow.
🔗
Recall the Rotational Law of Motion
\begin{equation*} \sum \tau = I\alpha \end{equation*}
The gravitational torque \(\tau = -Lmg\sin\theta(t)\) is the torque about the pivot point, \(I=mL^2 \) is the moment of inertia of a point mass about the pivot point and \(\alpha= \frac{d^2}{dt^2}\theta(t)\) is the angular acceleration of the pendulum mass. Putting this all together and simplifying:
\begin{equation} mL^2 \frac{d^2}{dt^2}\theta(t) = -Lmg \sin\theta(t) \tag{15.9.1} \end{equation}
\begin{equation} \frac{d^2}{dt^2}\theta(t)=-\frac{g}{L} \sin\theta(t) \tag{15.9.2} \end{equation}
This is the equation of motion for the pendulum in terms of the angular position as a function of time.
🔗
🔗

2. Analyzing the Equation of Motion.

Does your equation for \(\alpha\) satisfy the condition for Simple Harmonic Motion? Explain why or why not.
🔗
Solution.
The equation of motion for the simple pendulum does not satisfy the condition. The restoring force is not directly proportional to the angular displacement. Instead, it depends on \(\sin\theta\text{.}\)
🔗
🔗
🔗

3. Approximating the Restoring Force.

Use computer software to sketch graphs of \(\sin\theta\) and \(\theta\) on the same set of axes. Can you use the graphs to come up with a reasonable approximation in which the restoring force for the simple pendulum is directly proportional to the angular displacement?
🔗
Solution.
The Small-angle Approximation can be used to simplify the sine and cosine functions for small angles (see the Small-angle Approximation section for more details).
🔗
🔗
🔗

4. Analyzing the Equation of Motion.

Apply the Small-angle Approximation to simplify your expression for \(\alpha\) and use it to determine the oscillation frequency for the simple pendulum.
🔗
Solution.
Applying the small-angle approximation \(\sin\theta \approx \theta\) leads to
\begin{equation*} \frac{d^2}{dt^2}\theta(t)=-\frac{g}{L} \theta(t) \end{equation*}
from this and your model of Simple Harmonic Motion, the oscillation frequency is
\begin{equation*} \omega_p = \sqrt{\frac{g}{L}}\text{.} \end{equation*}
🔗
Definition 15.9.5. Simple Pendulum Model.
The angular frequency for a point mass \(m\) attached to a massless string of length \(L\) is
\begin{equation*} \omega_p = \sqrt{\frac{g}{L}} \end{equation*}
The equation of motion for the pendulum is given by
\begin{equation*} \theta(t) = \theta_{\text{max}} \cos(\omega_p t + \phi_o) \end{equation*}
🔗
🔗
🔗
🔗

5. Sensemaking.

Make sense of the angular frequency of the simple pendulum using units, numbers, and symbols.
🔗
🔗
🔗

References References

🔗
🔗
PrevTopNext