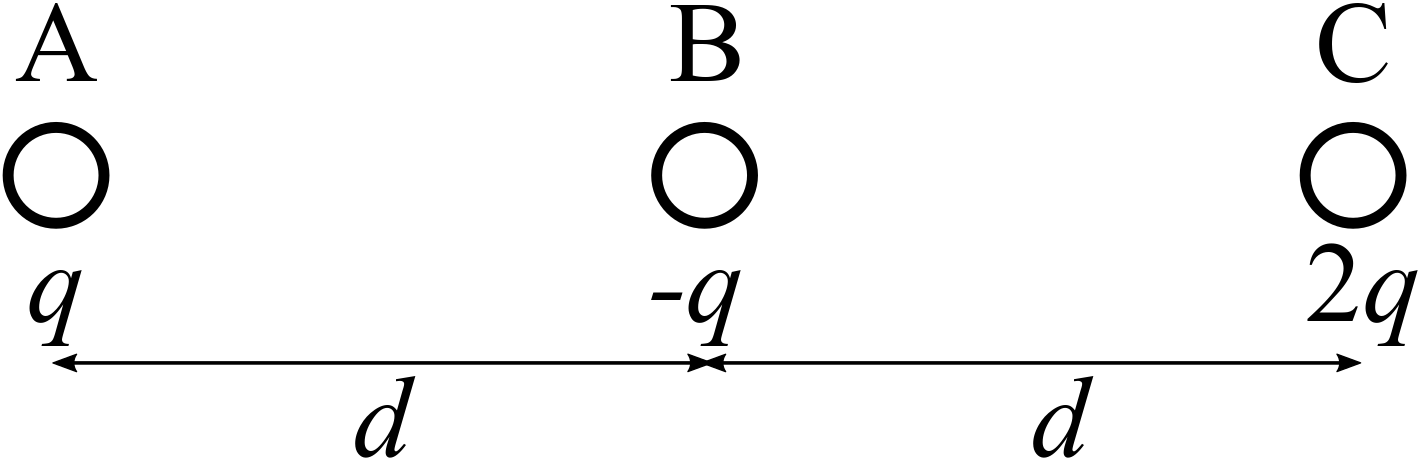Section20.8Electric Field of a Single Point Charge
Definition20.8.1.Single Point Charge.
The electric field created by a single point charge is
\begin{equation*}
\vec{E}(r) = k \frac {q}{r^2} \hat{r}
\end{equation*}
where \(q \) represents the source charge generating the field, \(r \) is the distance from the charge to the location you want to know the magnitude of the field, \(\hat{r} \) is a unit vector that points radially away from the source charge, and \(k = 9 \times 10^{9} \frac{\mathrm{Nm^2}}{\mathrm{C^2}}\) is a fundamental constant.
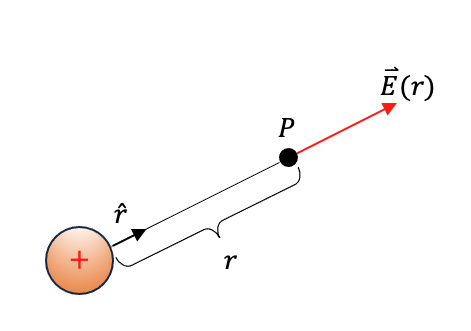
The figure below illustrates each of the quantities in the definition above. Consider a charge \(q \text{,}\) represented in the figure below by a positive charge, and a point in space \(P \) a distance \(r \) away from charge \(q \text{.}\) The vector symbol above the \(E\) tells you that the electric field is a vector and the \((r)\) indicates that it depends on, or is a function of, the distance \(r \) from the center of the charge \(q \) that creates the field. The field is defined at any point in space around the charge, and its magnitude changes with the inverse square of distance from that charge. To find the direction of the field, the unit vector \(\hat{r} \) always points away from the center of the charge, radially outward. Recall that a unit vector has magnitude \(|\hat{r}|=1.0 \) and so multiplying the equation by \(\hat{r} \) does not change the overall magnitude, it only tells you about the direction of the electric field at that point. If you choose a different point in space around the charge, both the magnitude and the direction of the electric field will be different depending on the position you choose.
Figure20.8.2.A visualization of the symbols used to define the electric field of a single point charge.
Note20.8.3.Charge subscripts.
Every electric charge generates an electric field. The term source charge is typically used to refer to a charge that is creating an electric field, represented as \(q_{\text{source}}\text{.}\) A source charge never feels a force from its own field. The term test charge, represented as \(q_{\text{test}}\text{,}\) is typically used to refer to the charge experiencing a force due to this field. It is common to drop the subscript notation and describe charges using just \(q\text{,}\) using context to determine which is the charge creating the field and which is the charge experiencing the field.
Note20.8.4.The Permittivity Constant.
In the equation above, the electric field is written in terms of the electrostatic constant, \(k = 9.0 \times 10^9 \frac{\mathrm{Nm^2}}{\mathrm{C^2}}\text{.}\) In other contexts, this constant is written as \(k = \frac{1}{ 4 \pi \epsilon_0}\text{,}\) where \(\epsilon_{0} = 8.85 \times 10^{-12} \frac{\mathrm{C^2}}{\mathrm{Nm^2}}\) is a fundamental constant known as the permittivity of free spsace.
The constant \(\epsilon_{0} \) (pronounced “epsilon naught”) is a constant of proportionality that scales how the magnitude of the electric field is related to charge and distance in a vacuum. If there is other matter around that charge, for example air or wood or water, that matter can affect how the electric field is permitted to exist, and thus the permittivity constant will be different.
Note20.8.5.Parallels to Gravity.
Recall the definition of The Gravitational Field. Note the units of the Gravitational constant and then recall the units of the electrostatic constant \(k \text{.}\) Do you notice any similarities?
ExercisesActivities
1.Electric Field Vector Maps.
Recall Practice Sketching Field Maps, in which you made a 2D-map of a vector field. The vector field you mapped is proportional to \(\hat{r}\text{!}\) Map this vector field and describe how this vector field changes (or stays the same) at different points in space. What do you think the map would look like if you could make it three-dimensional?
2.Explanation: Three Charges.
Shown below are three point charges (A, B, and C). Is the magnitude of the net electric force on charge A greater than, less than, or equal to the magnitude of the net electric force on charge C? Explain your reasoning.
