Section 1.1 Introduction to Vectors
A mathematical object which has a both a magnitude (a size or amount) and a direction is called a vector. It is essential to take into account how both the magnitude and direction of a vector quantity changes when you analyze motion. A quantity that only has a magnitude is called a scalar.
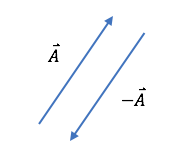
In diagrams, vectors are represented by arrows. The length of the arrow represents the magnitude of the vector and the arrowhead indicates the direction of the vector. Symbolically, you will draw an arrow on top of a symbol to denote a vector quantity.
Suppose you have a vector \(\vec{A}\) . The negative vector \(-\vec{A}\) has the same magnitude as vector \(\vec{A}\) , but points in the opposite direction. Once you understand how to visually represent and perform operations on vectors, you will move on to understand how to manipulate them algebraically.
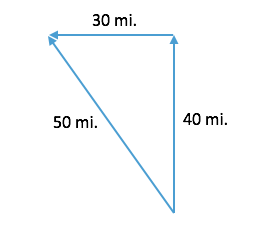
Suppose that you drive North for 40 miles and then head West for 30 miles. You have now driven a total of 70 miles, yet your total displacement is only 50 miles Northwest from where you started. Displacement is a vector quantity. It has a magnitude, 50 miles, and a direction (which happens to be 53 degrees north of west).
Another, common example of a vector is velocity. Velocity is a quantity that not only contains information about the speed of an object (the magnitude), velocity also gives information about the direction an object is moving. Speed does not have a "directionality" and can be fully described with just a number value. Therefore, speed is a scalar. For example, a speedometer reads a number, 60 km/hr, but gives no information about the direction of motion of the vehicle.
Exercises Activities
1. Explore Vectors and Scalars.
Make a list of physical quantities you are familiar with from your everyday experience. For each quantity, do you think it would be better to represent it as a scalar or as a vector?
2. Explore Magnitude.
A vector is typically represented graphically by an arrow. Which property of the arrow do you think represents the magnitude of the vector? How would you represent two vectors that have the same direction but different magnitudes?
References References
[1]
Vectors vs. Scalars by Dr. Michelle Tomasik from MIT 8.01 Classical Mechanics, Fall 2016, used under Creative Commons BY-NC-SA.
